Prime Reciprocals, Repetends and Repunits

I was recently watching a numberphile video on YouTube. Matt Parker explores a volume of work by William Shanks. Shanks calclulated the digit length of the repetend for the reciprocals of thousands of prime numbers. His work was carried out by hand in the mid to late 1800s.

A number is called prime if it is greater than 1 and has only 1 and itself as a divisor. The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. The following is c# code finds all primes less than 2^32 or 4,294,967,296 and saves them to a primes.bin.

private void DoIt(){
    BuildPrimeList(uint.MaxValue);
    BinaryWriter primeFile = new BinaryWriter(File.OpenWrite("primes.bin"));
    foreach(uint prime in m_PrimeList)
       primeFile.Write(prime);
    primeFile.Close();
}
 
private void BuildPrimeList(uint maxCandidate)
{
    m_PrimeList = new List<uint>();
    m_PrimeList.Add(2);
    for (uint i = 3; i < maxCandidate; i+=2)
       IsPrime(i);
}

private bool IsPrime(uint candidate)
{
    int maxFactor = (int)Math.Ceiling(Math.Sqrt(candidate))+1;
    foreach (int prime in m_PrimeList){
      if (candidate % prime == 0) return false;
      if (prime > maxFactor) break;
    }
    m_PrimeList.Add(candidate);
    return true;
}

The recipracol of a number n, is simply 1/n and when this fraction is converted to a decimal there are either finite digits or an infinite number of digits that repeat after some time. All prime numbers with the exception of 2 and 5 have decimal representations of their reciprocals containing infinite digits with repeating patterns. Consider the following examples:

When the pages of Shanks’ work appeared on the screen I noticed a relationship between some of the numbers. Many of the primes had a repeating digit count that was only one less then the prime number itself. Similar to 7 above. Then I noticed that some had half the repeating digits of one less than prime.

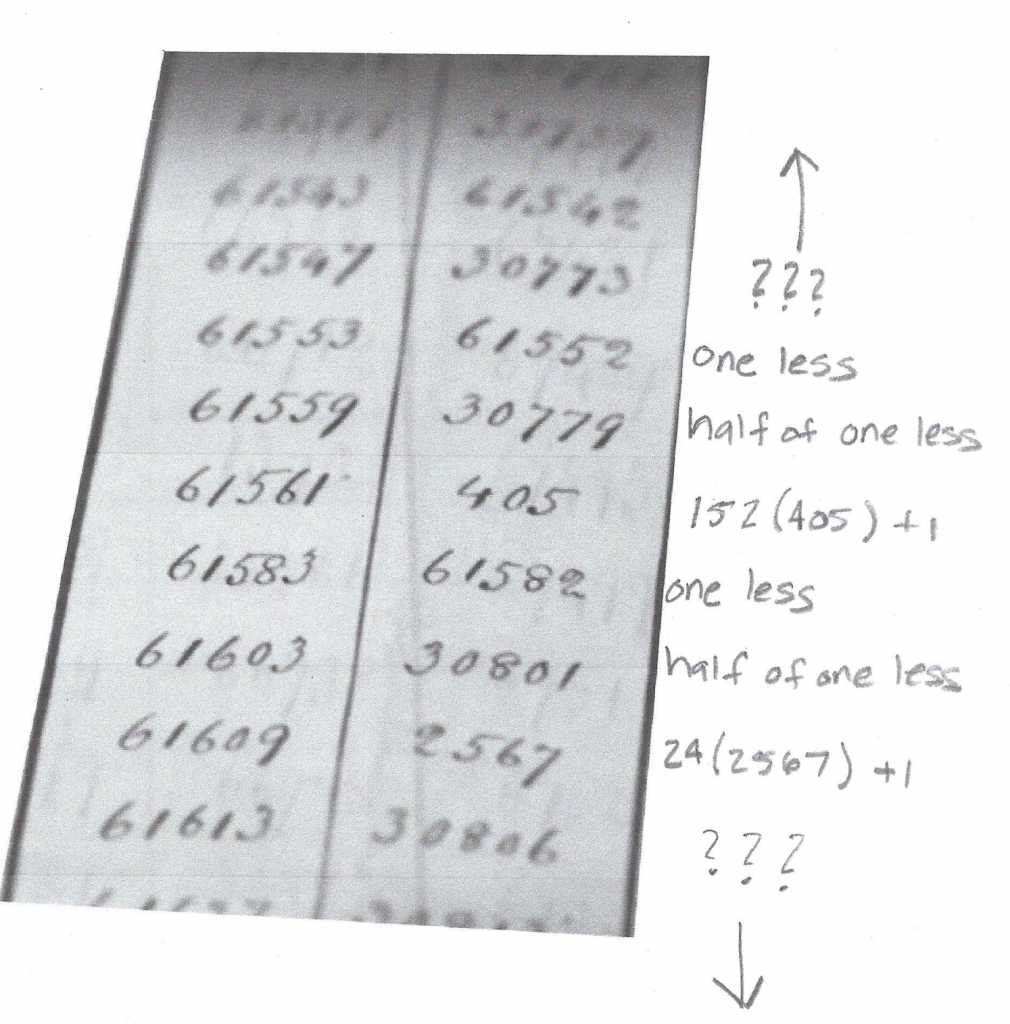
I paused the video and tested a few on the page and saw that each prime was one more than a multiple of the digit count. I supposed that this might be true for all the numbers in his list. Since I did not have his list available I decided to write the following code create a dictionary that would replicate his work. This way I could perform a test.

private uint RecipricolDigits(uint num, uint max)
{
   uint digitCount = 0;
   List<uint> used = new List<uint>((int)max);
   uint remainder = 1 % num;
   while (!used.Contains(remainder) && digitCount<=max){
     digitCount++;
     used.Add(remainder);
     remainder = (remainder*10) % num;
     }

   return digitCount;
}

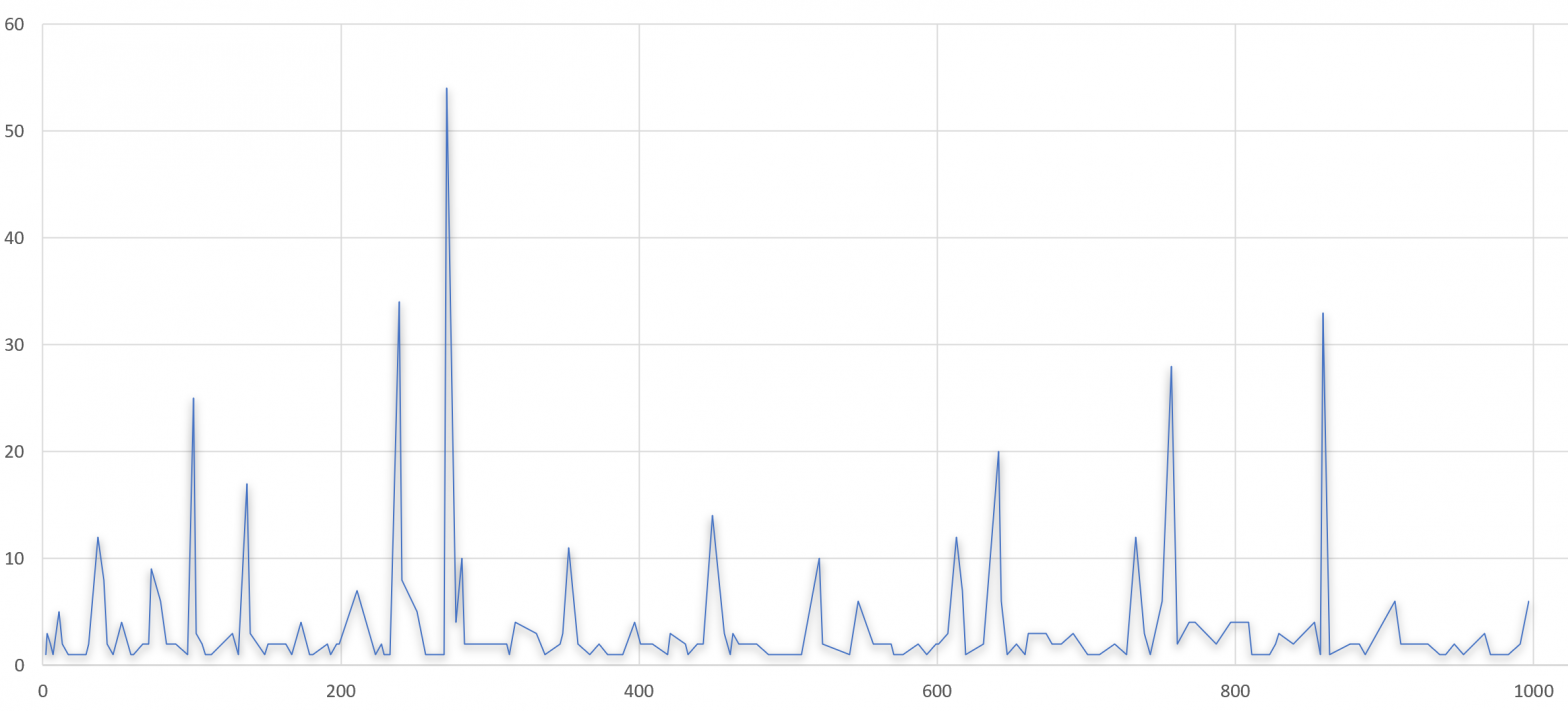
For each prime p<1000 I found that the prime was infact one more than a multiple of the number of repeating digits. I was curious if there might be a pattern to the multiples and decided to plot the against the prime number.

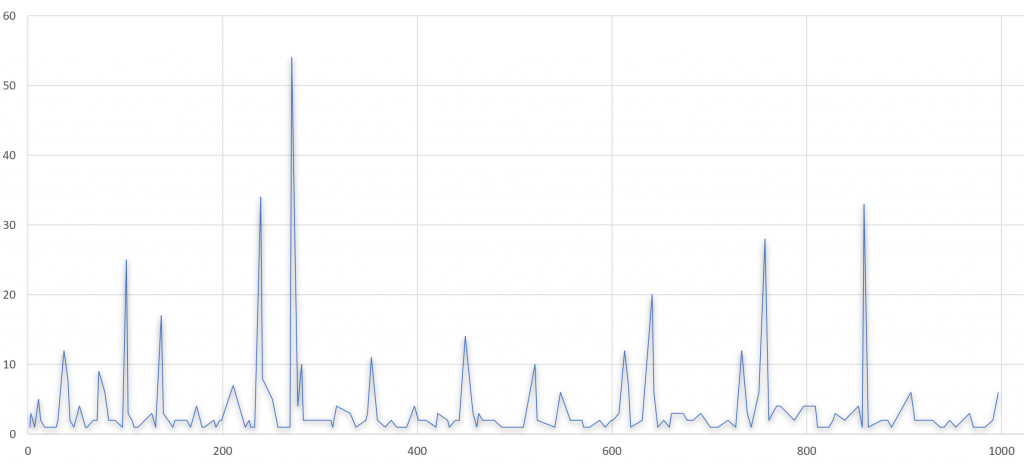
After deciding there was no obvious pattern I took interest in the spike represented by the prime 271. 1/271 in decimal form is 0.00369003690036900…. For a relatively large prime it only has 5 repeating digits and 54*(5)+1=271. At this point I decided to google 271 and found a wikipedia article containing that number.

This article discusses repunit numbers. All digits of a repunit number are 1 therefor 1 , 11, 111, 1111, 11111, …… are repunit numbers. 271 appeared in a list of prime factors of the first thirty base 10 repunit numbers.

Then I started to notice that all of the prime factors in the table had a low number of repeating digits within the decimal representation of its reciprocal. If one were to thumb through Shanks’ pages these repunit factors would definitely stand out as having few repeating digits. At this point I scripted some code that would calculate upto 265371653 rows of Shanks’ data and output a list ordered by the repeating digit count. The following is a partial list of primes in assending order of repeat counts for their reciprocals.

3         1
11        2
37        3
101       4
41        5
271       5
7         6
13        6
237       7
4649      7

73          8
137         8
333667      9
9091        10
21649       11
513239      11
9901        12
53          13
79          13
265371653   13

909091        14
31            15
2906161       15
17            16
5882353       16
2071723       17
19            18
52579         18
3541          20
27961         20

I was amazed and excited to see these numbers reflecting exactly those red numbers in the repunit factorization table from above! As the repunit numbers increase, so does the order that new prime factors appear! 3 being the only exception. I don’t have the computing power to test all primes up to numbers as high as 5363222357 and beyond in a timely matter, but even now as I write this blog I am noticing that the repeating digit count represents the repunit sequence number for which the prime will first appear!

R1 = 1
R2 = 11 = 11 (1/11 has 2 repeating digits)
R3 = 111 = 3 · 37 (1/37 has 3 repeating digits)
R4 = 1111 = 11 · 101 (1/101 has 4 repeating digits)
R5 = 11111 = 41 · 271 (1/41 and 1/271 have 5 repeating digits)
R6 = 111111 = 3 · 7 · 11 · 13 · 37 (1/7 and 1/13 have 6 repeating digits)
R7 = 1111111 = 239 · 4649 (1/239 and 1/4649 have 7 repeating digits)
R8 = 11111111= 11 · 73 · 101 · 137 (1/73 and 1/137 have 8 repeating digits)
R9 = 111111111 = 3² · 37 · 333667 (1/333667 has 9 repeating digits)
⋮

PAUSE!!!!! Stop writing this blog!

What? Why stop writing the blog? This is almost interesting for God’s sake! It is years later now and I have resolved to continue adding content to my site so now I will explain.

I was so excited that I might have discovered something original. What would it have felt like to sail the ocean blue and discover a new world? How would it feel when you found out you weren’t the first to discover it? I think this feeling has become common among many of us in the digital world. The experience of starting down what you percieve to be an original road only to realize you are within someone elses old tracks. There is a disappointment associated with learning that an idea is not original. This createive letdown caused me to put it all away and stop writing and stop exploring the repunit/prime recipricol relationship. As a result there would be no more insight, even if it was original, and there would be no more blog.

I discovered that my idea wasn’t original when reading a rather demoralizing sentence the history section of the aforementioned Wikipedia article.

"It was found very early on that for any prime p greater than 5, the period of the decimal expansion of 1/p is equal to the length of the smallest repunit number that is divisible by p."

I was able to glean the above “on my own” very quickly considering the youtube video and ensuing Wikipedia article were at my disposal, as well has having the power of a programming language and modern PC. The road to my “high” was quick and so was the fall.

William Shanks spent a lifetime creating his tables and I admire his dedication to such a tedious task and believe he must have found peace through his accomplishments.